导读

以航空发动机测量耙振动试验过程中的安全监测为需求。首先，基于测量耙结构特征简化模型，建立了含裂纹测量耙振动特征方程；其次，建立了某型测量耙有限元模型，通过数值模拟分析了裂纹参数（相对位置、裂纹长度）对测量耙固有频率的影响规律；最后，开展了该型测量耙的振动试验。扫频试验结果验证了测量耙有限元模型的准确性，测量耙在振动耐久性试验过程中出现孔边裂纹，固有频率降低了11.1%，表明在测量耙研制过程中开展振动考核试验时，可在试验现场通过试验前后固有频率的变化实时监测耙体的结构损伤。

引言

飞机及动力装置定型试飞中，通过测量耙或测头测量航空发动机各截面的压力和温度是重要的测试手段之一。测量耙主要承受着发动机气动力载荷、机匣振动载荷与热载荷，装机使用过程中一旦出现损伤，轻则测量耙不能正常工作，重则可能损伤发动机部件，危及飞行安全。测量耙研制过程中，通常需要对测量耙进行耐久振动试验，以评估测量耙结构承受振动的能力，验证其在工作环境下的结构完整性。目前，测量耙耐久振动过程中的结构完整性通常是振动试验结束后，采用X射线探伤进行裂纹损伤检测，但其周期长、花费大，因此耐久振动试验中能够快速诊断其裂纹损伤故障具有较大的工程意义。

由振动理论可知，裂纹的产生不仅导致构件的刚度降低，而且增加系统阻尼，影响系统的振动响应，所以通常运用构件的振动响应识别裂纹参数。研究者提出了多种含裂纹构件的振动响应分析方法。Ramesh等以裂纹深度与模态频率之间的函数关系为基础，分析了张开式裂纹梁的动力响应。Avramov等推导了有限自由度非线性动态系统，描述具有呼吸式裂纹悬臂梁的振动特性。Liu等提出了含呼吸式裂纹梁的二次非线性刚度模型，提出了含裂纹梁的非线性振动分析模型。文献［8-10］提出了基于固有频率的横向裂纹诊断模型，该模型将裂纹转换为一个无质量的弹簧单元。Calio等推导了一种含裂纹的Euler-Bernoulli梁动力响应解析方法。马一江等推导了含裂纹悬臂梁固有频率特征方程，从理论上说明裂纹位置、深度与固有频率的关系。Zai等通过试验研究了金属梁裂纹尺寸参数与固有频率的关系，随着裂纹深度的增加，其固有频率逐渐降低。马辉等建立直裂纹悬臂梁数值模型模拟了裂纹参数与固有频率的关系。

根据裂纹对构件振动响应的影响规律，研究者们提出了基于固有频率、基于模态振型、基于模态阻尼及基于频响函数等多种裂纹识别方法。Sayyad等采用理论与试验方法，研究了不同梁构件的裂纹参数识别方法。Elshamy等通过有限元及试验方法研究了悬臂梁裂纹位置、深度和材料对固有频率的影响，认为可通过固有频率的变化识别悬臂梁中的损伤。杨骁等基于Euler-Bernoulli梁振动模态的解析表达式，根据裂纹附加模态函数的构造特征，建立了一种新的裂纹损伤参数识别方法。闫少文等提出了一种基于非线性高频频响函数的无基准疲劳裂纹损伤识别方法。Lee提出了一种利用振动振幅识别梁中多裂纹的简单方法。Kam等基于振型和模态频率提出了裂纹识别无损方法。固有频率是振动参数中最易获得的振动特性，因此成为裂纹识别中最常用的参数之一。

针对测量耙振动试验过程中裂纹损伤的快速识别，笔者拟推导含裂纹测量耙的结构动力学方程，对基于固有频率变化的测量耙裂纹故障诊断方法进行研究，并在此基础上开展了该型测量耙的振动试验，探讨在振动试验现场基于固有频率快速识别测量耙结构损伤的可行性。

1 含裂纹测量耙的结构动力学方程

由测量耙常规结构特征及安装方式，可将测量耙简化为等截面悬臂梁，本节将用等截面悬臂梁代替测量耙来分析其结构动力学方程。裂纹梁模型如图1所示，长为l，截面为b×w。假定在悬臂梁表面任意位置存在一条深度为a的初始横裂纹，距离固定端为lc，且该横向裂纹始终保持张开。

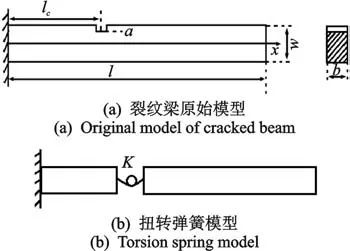
图1 裂纹梁模型

Fig.1 The model of cracked beam   根据Euler-Bernoulli梁理论，图1中等截面悬臂梁的振动微分方程可表示为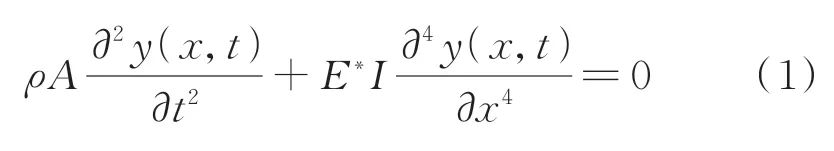  

其中：ρ为材料密度；A为该悬臂梁横截面面积；I为横截面惯性矩；E为材料弹性模量；E*为复弹性模量，E*=E(1+iγ)，γ为材料的阻尼损耗因子，i为虚数单位。   根据断裂力学基本原理，由于裂纹的存在，将影响悬臂梁裂纹处的局部柔度，因此可将该悬臂梁等效为由无质量扭转线弹簧或无质量弹性铰联接的两段弹性梁而构成的整体，实质上是将悬臂梁结构分为两子结构，而通过特殊的边界条件将两子结构联接起来。对裂纹的等效处理，目前国内外学者广泛采用的是无质量扭转线弹簧模型，裂纹的尺寸将直接影响等效扭转弹簧刚度系数K。Okamura等给出了与裂纹等效的扭转弹簧刚度系数计算及函数F(ζ)的表达式分别为

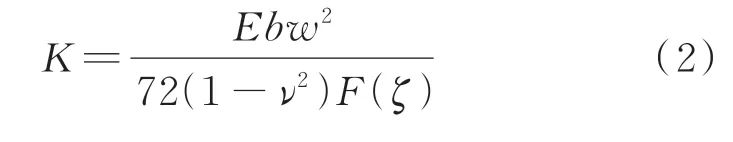
其中：ν为材料泊松比；b为悬臂梁宽度；w为悬臂梁厚度；ζ=a w，为裂纹相对深度（无量纲）。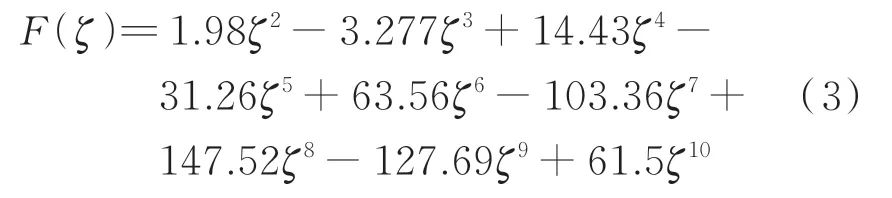  

由式（3）可以看出，函数F(ζ)是裂纹相对深度ζ的单一函数，进而裂纹等效扭转弹簧刚度系数K也是裂纹相对深度ζ的单一函数，通过式（2）建立起裂纹等效刚度与裂纹深度之间的函数关系。   根据模态分析方法，式（1）为4阶常系数线性齐次微分方程，可采用分离变量法求解。当该含裂纹悬臂梁自由振动时，其横向振动形式为

将式（4）代入到式（1）中，得到梁的振型表达式为

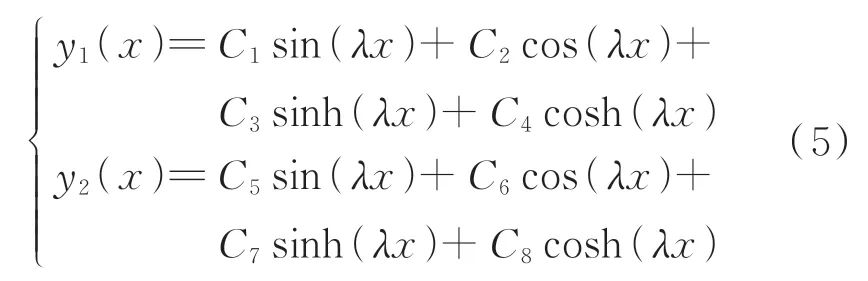
其中：λ为无量纲固有频率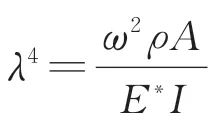，；ω为圆频率；C1，C2，…，C8为待定系数，可由图（1）中悬臂梁的边界条件确定。   参考文献［22］，图1中含裂纹悬臂梁边界条件为

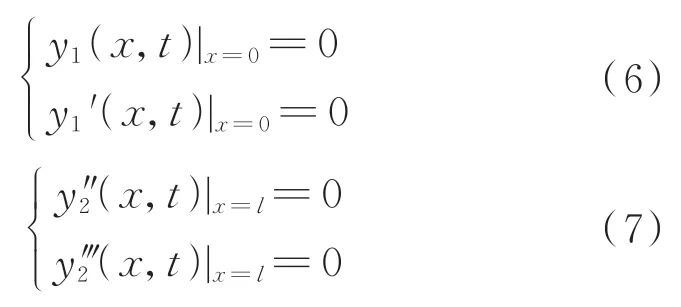
相应的连续条件为

斜率条件为

将边界条件式（6）～（9）代入式（5）中，求得待定系数C1，C2，…，C8的方程组，由待定系数方程有非零解条件求得含裂纹悬臂梁固有频率的特征方程为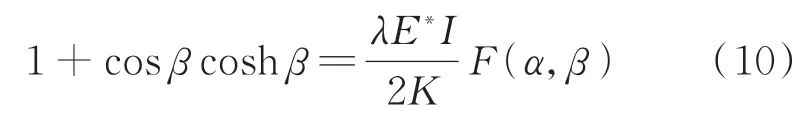  

函数F(α，β)的表达式为

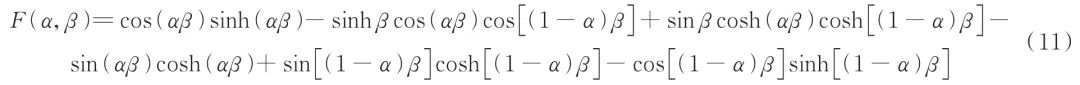  其中：α=lc l，为裂纹相对位置；β=λl。   对式（10）进行求解，可得到不同裂纹参数悬臂梁对应的固有频率特征方程。郭隆清基于控制变量法，将裂纹相对位置作为已知参数，对式（10）进行求解，得到含裂纹悬臂梁不同裂纹相对位置下裂纹相对深度对1阶固有频率的影响，如图2所示。

图2 裂纹相对深度对1阶无量纲固有频率的影响
Fig.2 Effect of relative crack depth on first-order dimensionless natural frequency

由图2可知，含裂纹悬臂梁结构的固有频率与裂纹参数（相对位置等）之间存在相互对应关系，可通过监测悬臂梁结构固有频率的变化来识别结构中裂纹参数。因此，可将该理论推广到航空发动机测量耙结构中，在测量耙振动考核试验时，通过实时监测测量耙固有频率的变化来诊断其裂纹故障的存在。  2 裂纹参数对测量耙结构动力学特性影响分析 2.1 测量耙结构特性分析

某风扇进口总压测量耙采用外装式设计，主要由主体骨架、安装座、测头及填充橡胶等部分组成，伸入流道部分为400 mm，最大厚度为20 mm，纵向截面积由耙体根部至顶部逐渐减小，以减轻结构重量。主体骨架和安装座均采用不锈钢材质加工而成，组焊后，采用注胶工艺形成变截面外形，注胶所用橡胶材料为硫化橡胶。基于有限元法对该测量耙进行模态分析，硫化橡胶假定为各向同性材料，材料参数为厂家提供，主体骨架及硫化橡胶材料的材料参数如表1所示。

表1 测量耙材料参数
Tab.1 Material parameters of rake

图3所示为测量耙前4阶模态振型分布，表2所示为测量耙对应的固有频率分布。通过振型分析可以发现，1阶及2阶振型均为弯曲振型，其中1阶为周向弯曲，2阶为气流方向（轴向）弯曲；3阶及4阶振型均为弯扭耦合振动。由于橡胶材料刚性远低于金属材料，其固有频率较低，因此高阶振动时橡胶部分存在明显局部振动。

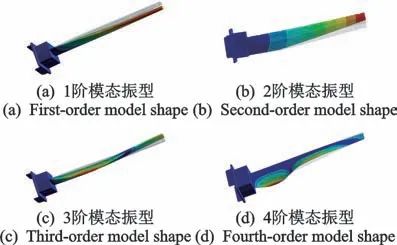
图3 测量耙前4阶模态振型
Fig.3 The first four model shapes of rake

表2 测量耙固有频率
Tab.2 Natural frequency of rake

图4为测量耙裂纹位置分布。为研究含裂纹测量耙的结构特性，基于测量耙有限元模型，在测量耙距离根部最近引气测头处，即图4（a）中1st处设置一裂纹。裂纹深度为2 mm，裂纹长度为6.4 mm，有限元模型中对裂纹处局部网格加密，网格尺寸设置为0.6 mm，如图4（b）所示。

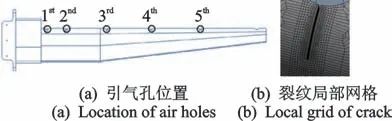
图4 测量耙裂纹位置分布
Fig.4 Crack location distribution of rake

对含裂纹测量耙进行模态分析，前2阶模态振型分布如图5所示，1阶及2阶振型均为弯曲振型，其中1阶为周向弯曲，2阶为气流方向（轴向）弯曲，与图3中前2阶振型分布一致，表明裂纹的存在并不影响测量耙振型分布。含裂纹测量耙固有频率分布如表3所示，与表2对比可知，该测量耙前4阶固有频率值均出现降低，但第2阶降低最为明显，降低7.4%，这是由于测量耙2阶弯曲振型为气流方向弯曲，能够最大限度的张开裂纹，降低整体刚性。

表3 含裂纹测量耙固有频率
Tab.3 Natural frequency of cracked rake

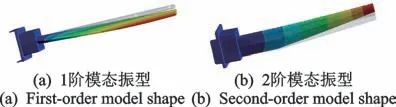
图5 含裂纹测量耙前2阶模态振型
Fig.5 The first two model shapes of cracked rake

由含裂纹测量耙与完整测量耙的振型及固有频率分布对比可知，裂纹的存在不影响测量耙的振型分布，但会导致其固有频率降低，且第2阶固有频率变化最为明显。因此，笔者在后续研究中，将主要以测量耙第2阶固有频率作为研究对象。  2.2 裂纹参数对测量耙固有频率影响规律  为研究裂纹位置对测量耙固有频率的影响，分别在测量耙距离根部较近的5个引气测头孔边处设置裂纹，裂纹位置如图4所示。设置的裂纹深度为2 mm，裂纹长度为4.5 mm。   定义测量耙伸入流道长度为l，将孔边裂纹距安装座距离与l之比定义为相对位置（无量纲），将含裂纹测量耙第2阶固有频率相对于表2中测量耙第2阶固有频率变化百分比定义为固有频率变化率。固有频率变化率与相对位置的关系如图6所示。由图可知，随着裂纹远离测量耙安装座，测量耙第2阶固有频率降低百分比逐渐减小，即固有频率逐渐增大，增大幅度逐渐减小。当裂纹逐渐接近测量耙自由端时，裂纹对测量耙固有频率的影响几乎可以忽略。

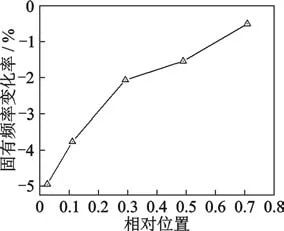
图6 裂纹相对位置与固有频率变化率的关系

Fig.6 Relationship between the relative position of crack and the change rate of natural frequency

为研究裂纹尺寸对测量耙固有频率的影响，在测量耙距离根部最近引气测头处，图4（a）中1st处设置如4（b）所示的裂纹。裂纹深度保持不变，但长度逐渐增加，分别设置为3.8，4.5，4.9，5.4和6.4 mm。   数值模拟后，裂纹长度与固有频率变化率关系如图7所示。由图可知，随着裂纹长度增加，测量耙固有频率的变化率值逐渐增大，第2阶固有频率逐渐下降。固有频率变化率与裂纹长度近似线性变化，拟合优度R2=0.998下的拟合方程为

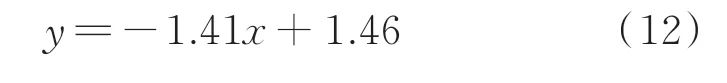
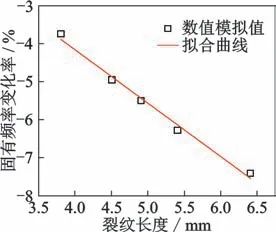
图7 裂纹长度与固有频率变化率的关系

Fig.7 Relationship between crack length and natural frequency change rate

3 某型测量耙裂纹损伤识别

裂纹的存在会导致测量耙固有频率明显下降，且裂纹参数不同，固有频率下降程度不同，本节将基于固有频率的变化识别测量耙振动试验过程中的损伤裂纹，以便及时中止试验，避免造成更大的危害。

3.1 测量耙振动试验方法

航空发动机测量耙振动试验采用电动振动试验台进行，测量耙振动试验如图8所示。

图8 测量耙振动试验
Fig.8 Vibration test of rake

图9为振动应变测试系统。为研究测量耙振动试验过程中振动应变响应及安全监测，需对测量耙表面进行应变计改装。根据强度理论分析应在测量耙根部张贴应变片，但根部区域灌注了橡胶材料，无法粘贴应变片。考虑到操作可实施性，选择在橡胶灌注区外的耙体金属结构上完成应变计改装。改装数量根据有限元初步分析结果选择应力较大区域3处进行粘贴。完成应变计改装并在耙体上组成测量电桥后，通过数据采集系统获取振动试验过程中的应变响应信号，用于测量耙振动监测及故障诊断。

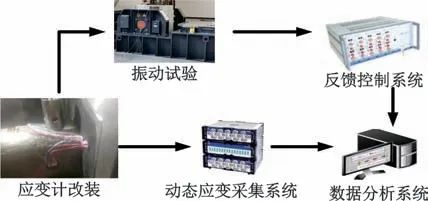
图9 振动应变监测系统
Fig.9 Vibration strain monitoring system

振动试验过程中，对测量耙y方向（y方向指测量耙测头进气垂直方向）仅进行耐久前扫频；z方向（z方向指测量耙测头进气方向）进行耐久前扫频、耐久振动、耐久后扫频3个试验。   耐久振动试验根据发动机转速分布，按照《涡轮发动机振动环境》图谱进行试验，燃气涡轮发动机振动谱如图10所示。试验前应仔细检查安装座与夹具之间的联接螺栓，确保足够的安装紧度。试验过程中，应密切注意数据分析系统中应变响应情况，以避免异常情况发生。

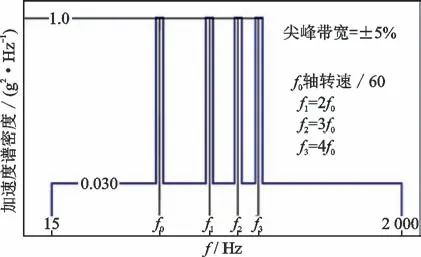
图10 燃气涡轮发动机振动谱
Fig.10 Vibration spectrum of gas turbine engine

3.2 扫频试验结果分析

测量耙耐久振动前应进行振动扫频试验，以测定其给定频率范围内的固有频率，通常对各方向上仅关注1阶固有频率。对测量耙进行应变计改装，振动试验过程中采用数据采集系统进行数据采集和分析，获取测量耙振动时应变随时间的响应。

图11所示为测量耙扫频过程中的应变响应经频谱分析后的1阶固有频率，其中y方向1阶固有频率为69.5 Hz，对应图3中1阶弯曲振型，z方向1阶固有频率为113.6 Hz，对应图3中2阶弯曲振型。将试验结果与表2中数值模拟结果对比可知，数值计算与试验测量固有频率的误差较小，y方向误差为3.0%，z方向误差为5.8%，验证2.1节中测量耙固有频率数值仿真的准确性，进一步验证了含裂纹测量耙数值仿真规律的合理性。

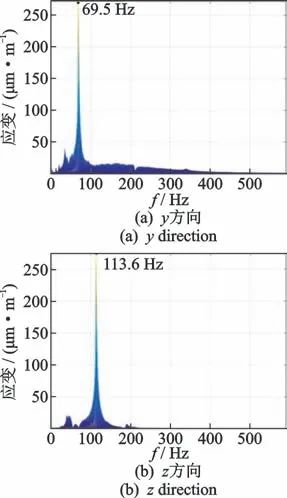
图11 耐久前测量耙1阶固有频率
Fig.11 The first-order natural frequency of rake before durability

3.3 测量耙损伤裂纹故障识别

z方向耐久前扫频结束后，按图10所示的振动功率谱密度进行测量耙耐久振动试验，试验中实时采集其应变响应，并通过图9中数据分析系统实时进行频谱分析。耐久振动试验进行一段时间后，发现测量耙固有频率如图12所示，固有频率为105.8 Hz，下降6.8%，可能是耐久振动试验对测量耙造成疲劳损伤，因此立刻中止z方向耐久振动试验。

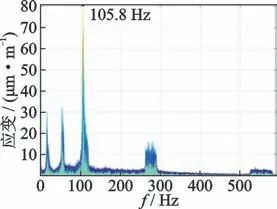
图12 耐久振动过程中固有频率
Fig.12 Natural frequency during durable vibration

耐久振动试验中止后，对测量耙进行4次z方向扫频振动试验，由采集器记录其应变响应，进行频谱分析后，固有频率见表4。   表4为耐久振动试验前后测量耙z方向1阶固有频率对比，由表可知，耐久试验前测量耙z方向1阶固有频率为113.6 Hz，耐久试验后z方向1阶固有频率均值为101.0 Hz，频率降低了11.1%，可能是测量耙产生裂纹，导致其刚性降低，进而固有频率降低。因此，对该测量耙测头孔边处仔细检查，并在靠近测量耙根部的引气测头孔边处发现已产生裂纹，具体裂纹尺寸分布如图13所示。

表4 测量耙耐久试验前后z方向频率对比
Tab.4 Comparison of Z-direction frequency before and after rake durable test

图13 测量耙根部裂纹分布
Fig.13 Crack distribution at rake root

测量耙振动试验过程中，通过振动应变监测系统对振动应变响应实时进行频谱分析，时刻关注测量耙固有频率的变化情况，能够快速、及时发现测量耙的裂纹故障，中止试验，对测量耙进行详细检查，以避免产生更大的故障。  4 结论  1）基于测量耙结构及安装方式，推导得到含裂纹测量耙结构动力学特征方程。   2）建立了测量耙固有频率数值模型，固有频率计算结果与试验相比最大误差为5.8%，验证了数值模型的准确性，并在此基础上开展了裂纹参数（裂纹位置、裂纹长度）对测量耙结构动力学特性的影响分析。结果表明：随着裂纹远离测量耙安装座，测量耙固有频率降低百分比逐渐减小；随着裂纹长度的增加，测量耙固有频率变化率近似线性降低。   3）通过分析振动试验过程中的应变响应，测量耙产生裂纹后固有频率降低了11.1%，固有频率变化明显，因此振动试验过程中可通过对固有频率的实时监测来诊断其裂纹故障，及时中止试验，避免更大的故障发生。